domingo, 22 de abril de 2012

Serie de Taylor


En matemáticas, una serie de Taylor de una función f(x) infinitamente derivable (real o compleja) definida en un intervalo abierto (a-r, a+r) se define como la siguiente suma:

La función exponencial (en azul), y la suma de los primeros n+1 términos de su serie de Taylor en torno a cero (en rojo).
f(x) = \sum_{n=0}^{\infin} \frac{f^{(n)}(a)}{n!} (x-a)^{n}
Aquí, n! es el factorial de n y f (n)(a) indica la n-ésima derivada de f en el punto a.
Si esta serie converge para todo x perteneciente al intervalo (a-r, a+r) y la suma es igual a f(x), entonces la función f(x) se llama analítica. Para comprobar si la serie converge a f(x), se suele utilizar una estimación del resto del teorema de Taylor. Una función es analítica si y solo si se puede representar con una serie de potencias; los coeficientes de esa serie son necesariamente los determinados en la fórmula de la serie de Taylor.
Si a = 0, a la serie se le llama serie de McLaurin.
Esta representación tiene tres ventajas importantes:
  • La derivación e integración de una de estas series se puede realizar término a término, que resultan operaciones triviales.
  • Se puede utilizar para calcular valores aproximados de la función.
  • Es posible demostrar que, si es viable la transformación de una función a una serie de Taylor, es la óptima aproximación posible.
Algunas funciones no se pueden escribir como serie de Taylor porque tienen alguna singularidad. En estos casos normalmente se puede conseguir un desarrollo en serie utilizando potencias negativas de x (véase Serie de Laurent. Por ejemplo f(x) = exp(−1/x²) se puede desarrollar como serie de Laurent.

Series de Maclaurin (Taylor alrededor de 0) notables


La función coseno.

Una aproximación de octavo orden de la función coseno en el plano de loscomplejos.

Las dos imágenes de arriba puestas juntas.
A continuación se enumeran algunas series de Taylor de funciones básicas. Todos los desarrollos son también válidos para valores complejos de x.


Función exponencial y logaritmo natural

e^{x} = \sum^{\infin}_{n=0} \frac{x^n}{n!}\quad, \forall x; n \in \mathbb{N}_0
\ln(1+x) = \sum^{\infin}_{n=1} \frac{(-1)^{n+1}}n x^n\quad\mbox{, para } \left| x \right| < 1

[editar]Serie geométrica

\frac{1}{1-x} = \sum^{\infin}_{n=0} x^n\quad\mbox{ para } \left| x \right| < 1


Teorema del binomio

(1+x)^\alpha = \sum^{\infin}_{n=0} \frac{\Gamma(\alpha+1)}{\Gamma(n+1)\Gamma(n-\alpha)} x^n\quad para \left| x \right| < 1\quad
y cualquier \alpha\quad complejo


Funciones trigonométrica

\sin x = \sum^{\infin}_{n=0} \frac{(-1)^n}{(2n+1)!} x^{2n+1}\quad, \forall x
\cos x = \sum^{\infin}_{n=0} \frac{(-1)^n}{(2n)!} x^{2n}\quad, \forall x
\tan x = \sum^{\infin}_{n=1} \frac{B_{2n} (-4)^n (1-4^n)}{(2n)!} x^{2n-1}\quad, \mbox{ para } \left| x \right| < \frac{\pi}{2}
Donde Bs son los Números de Bernoulli.
\sec x = \sum^{\infin}_{n=0} \frac{(-1)^n E_{2n}}{(2n)!} x^{2n}\quad\mbox{, para } \left| x \right| < \frac{\pi}{2}
\csc{x}=\sum_{n=1}^\infty{\frac{2(2^{2n-1}-1)B_{n}x^{2n-1}}{(2n)!}}\quad\mbox{, para } 0<\left |{x}\right |< \pi
\arcsin x = \sum^{\infin} \frac{(2n)!}{4^n (n!)^2 (2n+1)} x^{2n+1}\quad\mbox{, para } \left| x \right| < 1
\arctan x = \sum^{\infin} \frac{(-1)^n}{2n+1} x^{2n+1}\quad\mbox{, para } \left| x \right| < 1


Funciones hiperbólicas

\sinh x = \sum^{\infin}_{n=0} \frac{1}{(2n+1)!} x^{2n+1}\quad , \forall x
\cosh x = \sum^{\infin}_{n=0} \frac{1}{(2n)!} x^{2n}\quad , \forall x
\tanh x = \sum^{\infin}_{n=1} \frac{B_{2n} 4^n (4^n-1)}{(2n)!} x^{2n-1}\quad\mbox{, para } \left| x \right| < \frac{\pi}{2}
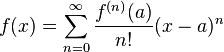
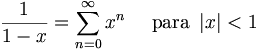
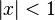
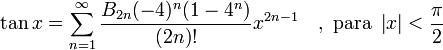
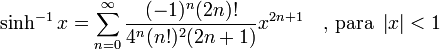
\sinh^{-1} x = \sum^{\infin}_{n=0} \frac{(-1)^n (2n)!}{4^n (n!)^2 (2n+1)} x^{2n+1}\quad\mbox{, para } \left| x \right| < 1
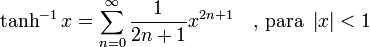
\tanh^{-1} x = \sum^{\infin}_{n=0} \frac{1}{2n+1} x^{2n+1}\quad\mbox{, para } \left| x \right| < 1
http://www.unizar.es/analisis_matematico/analisis1/apuntes/09-seriespotencias.pdf

Publicado por en

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)